SC junctions
超伝導接合系とは超伝導体と他の物質とを接合した系のことです。 超伝導体はフェルミ面上にエネルギーギャップを持ち、このギャップの構造に起因した量子干渉効果によって多彩な現象が生じます。応用上の観点では、超伝導体を使ったデバイスの特性は超伝導物質単体の性質だけではなく、接合界面の特性にも大きく影響されます。このことから超伝導接合系の研究は新奇量子デバイス開発の観点から極めて重要です。
-
常伝導体/超伝導体接合とアンドレーエフ反射 ▼
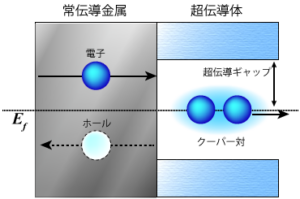 常伝導体・超伝導体接合においては、常伝導金属から入射した電子のエネルギーが超伝導体のエネルギーギャップ内にある場合は、 準粒子としてトンネルすることができません。超伝導体との界面では通常の反射だけではなくて、 入射した電子が超伝導体との界面で正孔(ホール)として反射されるアンドレーエフ反射が存在します。 アンドレーエフ反射により、超伝導体中にクーパー対が形成されます。 この過程は1964年Andreevにより予言され、常伝導体・超伝導体接合の輸送特性を理解するうえで不可欠なものとなっています。 アンドレーエフ反射の理論を超伝導体接合の輸送特性に拡張したのが1982年のBlonder, Tinkham, Klapwijkの理論でした。 接合の透過率が1の場合には完全アンドレーエフ反射が起こり、透過率が低くなるとアンドレーエフ反射の確率は抑制されます。
常伝導体・超伝導体接合においては、常伝導金属から入射した電子のエネルギーが超伝導体のエネルギーギャップ内にある場合は、 準粒子としてトンネルすることができません。超伝導体との界面では通常の反射だけではなくて、 入射した電子が超伝導体との界面で正孔(ホール)として反射されるアンドレーエフ反射が存在します。 アンドレーエフ反射により、超伝導体中にクーパー対が形成されます。 この過程は1964年Andreevにより予言され、常伝導体・超伝導体接合の輸送特性を理解するうえで不可欠なものとなっています。 アンドレーエフ反射の理論を超伝導体接合の輸送特性に拡張したのが1982年のBlonder, Tinkham, Klapwijkの理論でした。 接合の透過率が1の場合には完全アンドレーエフ反射が起こり、透過率が低くなるとアンドレーエフ反射の確率は抑制されます。 -
ジョセフソン接合 ▼
超伝導体と超伝導体を接合した系においては、2つの超伝導体の持つ巨視的な位相差に依存した超伝導電流が流れます。 この電流は電圧をかけなくても流れる無散逸な流れです。 この画期的な効果は、1962年にジョセフソンによって予言され、その後多くの実験が行われています。 2つの超伝導体の透過率が低い場合はdcジョセフソン電流は、sinφ に比例しますが、 透過率が高くなると高調波 sin(nφ) の効果が重要になり、電流位相差依存性を描いた際の波形は典型的なsinの形から大きくずれます。 ジョセフソン効果の理論研究はいろいろと行われて今したが、 90年代初頭に古崎・塚田によってアンドレーエフ反射係数を使って系統的にジョセフソン電流を表現する理論が登場して以降、大きく発展しました。
-
アンドレーエフ束縛状態 ▼
超伝導の接合系や磁束芯などの不均一な超伝導系では電子とホールの干渉によりアンドレーエフ束縛状態(ABS)とよばれるギャップ内状態が存在することが60年代から知られていました。 超伝導体・超伝導体のジョセフソン接合においてはアンドレーエフ束縛状態を用いて、 ジョセフソン電流を記述できることがあることは、90年代のビーネッカーらの研究で知られています。 スピン1重項の超伝導体においては、超伝導体表面においては一般にはアンドレーエフ束縛状態は存在しません。 しかし、銅酸化物超伝導体等の異方的超伝導体においては(銅酸化物超伝導体のクーパー対の対称性はd波ということが明らかになっています)、 表面に零エネルギー(ミッドギャップ)状態が形成されます。 零エネルギー状態は、常伝導金属・超伝導体接合におけるトンネル分光における零バイアス電圧のコンダクタンスピークとして現れて、 その存在は異方的超伝導体を特徴づけるものとして今日広く知られています。 異方的超伝導体のトンネル分光の研究はその後発展して、今日のマヨラナフェルミオンの研究へとつながっています。
関連論文
- Y. Tanaka and S. Kashwiaya, Phys. Rev. Lett. 74 3451 (1995).
- S. Kashiwaya and Y. Tanaka. Rep. Prog. Phys. 63 1641 (2000).
- Y. Tanaka, T. Yokoyama and N. Nagaosa, Phys. Rev. Lett. 103, 107002 (2009).
-
近接効果 ▼
金属と超伝導体を接合した系では、金属の中にクーパー対が侵入します。 この効果を近接効果と呼びます。アンドレーエフ反射を作り出す電子・ホールの干渉効果と近接効果は表裏一体をなすものであります。 金属が拡散伝導領域にあるときは、金属・超伝導体の接合系の抵抗はバルクの金属の値と界面抵抗の単純な和とはなりません。 侵入したクーパー対のために金属の抵抗は一般に小さくなります。 このような近接効果による抵抗の計算を行う際にはUsadel方程式を用いた方法が大変に有効です。 もともとLarkinらによって開発されていましたが、90年代メゾスコピック超伝導の進歩によって進展して、 Volkov、Nazarovらによって発展しました。
-
奇周波数クーパー対 ▼
超伝導状態を担うクーパー対は2電子から構成されることが広く知られています。 クーパー対の対称性に関して、多くの教科書には次のようにかかれています。 フェルミ・ディラック統計に従う2電子の対関数(ペア振幅)が、 それを構成する2電子の同時刻での入れ替えに関して反対称でなくてはなりません。 なぜなら、フェルミ・ディラック統計と整合しないといけないからです。 クーパー対の対称性は、スピン1重項偶パリティ(例えばs波やd波)とスピン3重項奇パリティ(p波 など)に分類されます。 この分類では、同一時刻で形成されるクーパー対(2電子の相関)に関して着目していることになります。 しかし、対関数を2電子の相対時間に関してフーリエ変換し周波数表示にしたとき、 対関数が周波数依存性を持つことも原理的には可能です。 そのような場合は、スピン3重項偶パリティ、スピン1重項奇パリティと分類されます。 まとめると対関数が周波数の偶関数になっているならば、 クーパー対の対称性は従来通りスピン1重項偶パリティとスピン3重項奇パリティに分類され、 対関数が周波数の奇関数となるとスピン3重項偶パリティ、スピン1重項奇パリティと分類されます。 そして可能なクーパー対の分類は次の表のようになります。
周波数(時間) スピン 軌道 全体 超伝導状態 ESE +(偶) ー(一重項) +(偶) ー(奇) 金属超伝導, 銅酸化物 ETO +(偶) +(三重項) ー(奇) ー(奇) ヘリウム3, Sr2RuO4 OTE ー(奇) +(三重項) +(偶) ー(奇) バルクでは未確認 OSO ー(奇) ー(一重項) ー(奇) ー(奇) バルクでは未確認 ESE,ETO,OTE,OSOは、それぞれ、偶周波数スピン1重項偶パリティ、偶周波数スピン3重項奇パリティ、 奇周波数スピン3重項偶パリティ、奇周波数スピン1重項奇パリティを表しています。 奇周波数クーパー対(OTEのs波)は1974年にBerezinskiiによって提案されました。 バルクの超伝導状態でこのような対の実現を考えるのは難しく、まだ奇周波数バルク超伝導体は発見されていません。
しかし、対称性の破れにより、主要なクーパー対は従来の偶周波数のペアであっても奇周波数のペアがSubdominantなペアとして混ざることは可能です。 並進対称性の破れにより、不均一な超伝導体においては、奇周波数クーパー対が偶周波数クーパー対に混在して普遍的に存在することが明らかになりました。
バルクの対称性 アンドレーエフ束縛状態 界面での対称性 ESE(s, dx2-y2-wave) 
No ESE+(OSO) ESE(dxy-wave) 
Yes OSO+(ESE) ETO(px-wave) 
Yes OTE+(ETO) ETO(py-wave) 
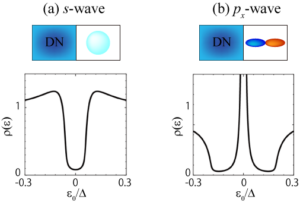
No ETO+(OTE) バルクの対称性と界面(表面)での対称性は上の表のようにまとまります。 またミッドギャップ・アンドレーエフ束縛状態の実体は、奇周波数クーパー対そのものです。 d波超伝導体表面のミッドギャップ・アンドレーエフ束縛状態は奇周波数p波であるのに対してp波超伝導体表面のそれは奇周波数s波になります。 そのために、スピン3重項p波超伝導体・常伝導金属接合においては、界面に形成された奇周波数s波が常伝導領域(不純物散乱が顕著な拡散伝導領域)に浸入する異常な近接効果が起こります。 この異常な近接効果は準粒子状態密度ρが零エネルギーでピークをもつ極めて特異なもので(下図)、従来から知られている準粒子状態密度が零エネルギーでギャップを持つ近接効果とは全く異なります。 奇周波数ペアが存在すると異常な電磁応答現象が期待され、この観点から広く研究されています。
関連論文- Y. Tanaka, A. A. Golubov, S. Kashiwaya, and M. Ueda: Phys. Rev. Lett. 99 (2007) 037005.
- Y. Tanaka, Y. Tanuma, and A. A. Golubov: Phys. Rev. B 76 (2007) 054522.
- Y. Tanaka and A. A. Golubov: Phys. Rev. Lett. 98 (2007) 037003.
- Y. Tanaka and S. Kashiwaya: Phys. Rev. B 70 (2004) 012507.
- Y. Asano, A. A. Golubov, Y. V. Fominov, and Y. Tanaka: Phys. Rev. Lett. 107 (2011) 087001.
- T. Yokoyama, Y. Tanaka, and N. Nagaosa: Phys. Rev. Lett. 106 (2011) 246601.
- Y. Tanaka, Y. Asano, A. Golubov, and S. Kashiwaya: Phys. Rev. B 72 (2005) 140503(R).
- Y. Tanaka, M. Sato and N. Nagaosa, J. Phys. Soc. Jpn., 81, 011013 (2012).
-
発現機構 ▼
超伝導とは、転移温度以下において電気抵抗が0になる現象であり、1911年にHeike Kamerlingh Onnesによって発見されました。 金属の常伝導相において仮想的に電気抵抗が0とした状態(完全伝導状態)とは異なり、マイスナー効果と呼ばれる完全反磁性を示すことが1933年に発見され、 常伝導状態とは異なる物質の新しい相であることが決定付けられています。 一方で、超伝導が発現する理由、及び超伝導状態における電子状態は、超伝導の発見以来長きに渡って不明でした。 しかし、1957年にBardeen, Cooper, Schriefferの3名によって発表された理論(BCS理論)によって、超伝導発現機構理論の基本が明らかになりました。 以下では、そのBCS理論について簡単に説明を行います。
まず、超伝導状態においては、電子二つが対を組んでいます。 この対をクーパー対と呼びます。電子はフェルミ粒子ですが、電子二つが対を組んだクーパー対はボソンとなるため、クーパー対が集団で凝縮することが出来ます(ボーズ凝縮)。 この凝縮状態が超伝導状態であると言えます。 では、どのようにすれば電子がクーパー対を形成することが出来るのでしょうか?電子が対を組むためには電子間に何らかの引力が働く必要があります。 電子同士は元々クーロン斥力が存在するので、そのままではクーパー対を形成することが出来ません。 超伝導状態においては、電子間のクーロン斥力を有効的に引力にする必要があります。BCS理論においては、この引力の形成機構としてフォノンを取り上げました。 負の電荷を持つ電子が、正の電荷を持つ原子核が並んだ結晶中を運動すると、結晶格子に歪みが起こります(フォノン)。 歪んだ部分においては他の部分に比べて正の電荷に偏っているので、別の電子がその偏った場所に有効的な引力を感じます。 つまり、電子間には、フォノンを媒介として有効的な引力が働いていることになります。 この有効的な引力によってクーパー対が形成され、それが凝縮することによって超伝導状態となるのです。

このように、BCS理論によって超伝導の基本的な発現機構が明らかにされました。 ところが、BCS機構の超伝導体とは明らかに性質の異なる超伝導体(非従来型超伝導体)が、1978年の重い電子系超伝導体の発見を契機として次々と見つけられました。 その代表例が1986年に発見された銅酸化物高温超伝導体です。 高温超伝導体においては、クーパー対を作る引力は電子-格子相互作用ではなく、電子の持つスピンが隣同士で反平行になろうとするスピン揺らぎであると言われています。 2008年に発見された鉄系超伝導体は銅酸化物に次ぐ高い転移温度を持った超伝導体ですが、スピン揺らぎの他に軌道揺らぎを媒介とした超伝導理論が提案されています。
その他、銅酸化物超伝導体と同じ結晶構造を持つSr₂RuO₄においては、クーパー対を形成する電子が互いに平行となるスピン三重項状態であることが実験的に観測されていまが、 その発現機構については様々な理論が提案されており、決着はついていません。 また、近年、トポロジカル絶縁体にキャリアドープしたCuxBi2Se3において超伝導が発見されました。 この物質はトポロジカル超伝導の候補物質として注目を浴びていますが、その発現機構については未だ明らかになっておりません。 当研究室においては、このような超伝導がクーパー対を作る仕組み=超伝導発現機構について研究を行っております。
Topological materials
トポロジカル構造とは、連続変形でほどけない空間的な「場」の構造を指します。一般にトポロジカル不変量と呼ばれる整数で分類され、不変量の違う構造は連続的に移り変わることができません。 このように説明すると、数学的でとっつきにくい話に思いがちですが、図を書いて考えると実は非常に明快な概念です。
例として2次元空間における古典XYスピンを考えてみましょう。秩序変数、すなわち「場」は、磁化の方向を表すxy面内を向いた単位ベクトルで、そのベクトルの動き得る自由度(「秩序変数空間」と呼びます)は単位円で表現できます。 ここで、図(a)-(c)にあるような磁化の空間構造を考えます。どれも中心では磁化の方向が決まらない欠陥です。 これらをトポロジカルに分類するために、欠陥を囲うように黄色い矢印に沿って磁化方位の変化を調べます。 各図の横に秩序変数空間で磁化方位がどう変化するかを示しており、(a) (b)では反時計回りに単位円を一周するのに対し、(c)では時計回りに一周します。 (a)と(b)は回る向きが同じなので、これらの構造は連続変形で移り変わることができ、実際に(a)の磁化構造を各点で画面に垂直な軸の周りに90度回転させると(b)になります。 一方、(c)は(a)(b)と周る向きが逆向であるため、(a)(b)とは連続的に移り変わることができません。つまり、(a)(b)はトポロジカルに等価な構造、(c)はトポロジカルに異なる構造、となります。 この例の場合、実空間で欠陥を一周する間に、秩序変数空間を何周するかという「巻付き数」で構造を分類することができ、(a)(b)は巻付き数1、(c)は巻付き数-1となります。 この巻付き数がトポロジカル不変量です。XYスピン以外にも、秩序変数空間が単位円で記述できる系(s波超伝導、超流動ヘリウム、液晶など)であれば、全く同じ議論で欠陥を分類することができ、トポロジカルな分類は系に依らない普遍的な概念となっています。
次に、上記の話を拡張して、3次元空間における3次元単位ベクトル(ハイゼンベルグスピン)のトポロジカル構造を考えてみましょう。 この場合の秩序変数空間は3次元単位ベクトルの方向を示す単位球です。 3次元空間に点欠陥があると、点欠陥を覆う球面を一回りする間に場の空間である単位球を何回覆うかという数で構造が分類されます。 具体例としては図(d)のようなものがあり、モノポールと呼ばれます。
モノポールを囲んでいる球面を2次元平面に展開すると、スカーミオンと呼ばれる面白い構造が得られます。 具体的には、図(e)に示すような射影を考えます。つまり、単位球の北極と球面上の点(赤丸)を直線で結び、南極に接した平面とこの直線の交わる点(青点)に赤丸の点での磁化を置きます。 (複素関数に詳しい人は、複素平面とリーマン球の関係を思い出してください。)このようにしてできるのが図(f)の構造です。 これは、欠陥を伴わない2次元のトポロジカル構造となっていて、境界で磁化が上を向いているという境界条件を課すことによって安定に存在します。 (a)(b)がトポロジカルに等価だったのと同様に、(f)(g)もトポロジカルに等価で、どちらもスカーミオン、またはスキルミオンと呼ばれ、現在物性分野で盛んに研究されています。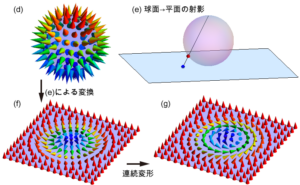
-
トポロジカル絶縁体・トポロジカル結晶絶縁体 ▼
トポロジカル絶縁体
固体中の電子の波動関数から定義されるトポロジカル不変量が非自明な値をとっている絶縁体をトポロジカル絶縁体と呼んでいます。 その表面には安定な金属状態が現れますが、れはトポロジカル不変量によってその存在が保証されているものです。さらに、トポロジカル不変量は系の電磁応答・輸送現象における物理量にもなっています。トポロジカル絶縁体の代表的な例は磁場中の二次元電子系において生じる量子ホール効果です。 この場合には量子ホール伝導度がトポロジカル不変量であり、その値に応じて系の端には金属状態が存在し、永久電流が流れています。 量子ホール効果は古くから知られている例でしたが、近年になってそのスピン版である量子スピンホール効果、さらには三次元系におけるトポロジカル絶縁体が発見され、以降、この分野の研究が爆発的に加速することになりました。 興味深いことに、三次元のトポロジカル絶縁体においては電場(磁場)によって磁化(電気分極)が誘起される電気磁気効果が生じ、 さらに、その分極率がトポロジカル不変量で表される(=量子化されている)ことが予言されています。
トポロジカル結晶絶縁体
量子スピンホール絶縁体や三次元のトポロジカル絶縁体は時間反転対称性に保護されたZ2トポロジカル不変量をもち、また、これに対応して表面金属状態が存在しています。 一方、時間反転対称性の代わりに、回転や鏡映といった結晶の対称性によってもトポロジカル不変量を定義できることも分かっています。 このトポロジカル不変量が非自明な値をとっている系をトポロジカル結晶絶縁体(topological crystalline insulator)と呼んでいます。実際に、2012年にはⅣ-Ⅵ族半導体において、鏡映対称性によるトポロジカル結晶絶縁体状態が実現していることが実験的に明らかになりました。これに留まらず、様々な物質の予言やその分類理論も提案され、更に研究が加速してきています。
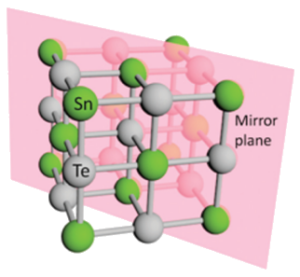
関連論文- Y. Tanaka, et al., Nat. Phys. 8, 800 (2012); S.-Y. Xu, et al., Nat. Commun. 3, 1192 (2012); P. Dziawa, et al., Nat. Mater. 11, 1023 (2012).
-
トポロジカル超伝導体・トポロジカル結晶超伝導体 ▼
トポロジカル超伝導体
電子がクーパー対を形成すると、電子と正孔の間の混成が生じ、フェルミ面上にエネルギーギャップが開きます。 この状態は超伝導体と呼ばれており、多くの金属が低温で超伝導状態へと相転移することが知られています。 超伝導体の基底状態では、フェルミエネルギー以下の状態は完全に詰まっており、フェルミオン励起を作るのに有限のエネルギーが必要であるため、絶縁体と類似の状態が実現されています。 この類似性から、超伝導状態に対しても、トポロジカル絶縁体と同様に基底状態の波動関数のトポロジカル数がノンゼロである状態が実現でき、トポロジカル超伝導体と呼ばれています。 トポロジカル超伝導体は、その表面にマヨラナ励起と呼ばれる自分自身が反粒子となっているディラック励起を持つのが特徴です。
トポロジカル結晶超伝導体
超伝導体を実現する物質は、その物質固有の結晶対称性を持っています。 この結晶対称性によって新たなトポロジカル数を導入することができます。 スピン縮退をしている通常の電子系では、トポロジカル超伝導体特有のマヨラナ励起はかならず対で現れ、 ディラック励起と同じ自由度を持つため、マヨラナ励起特有の性質を実証するのは難しいと考えられてきましたが、 結晶対称性を用いることで、マヨラナ励起特有の性質が検証可能であることが明らかになっています。
-
非可換統計とマヨラナフェルミオン ▼
非可換統計
数学では、ある代数に従う要素の演算が順番を問わないとき、これらは可換であると言い、交換法則が成り立たない場合は、非可換であるといいます。例えば、n×n行列(n>1)は一般的に非可換です。 非可換統計とは、ある種の粒子が従う統計性のことを指します。三次元空間では、粒子 の統計性は基本的にボーズとフェルミ統計に分かれ、それらの統計性に従う粒子はそれぞれボソ ンとフェルミオンと呼ばれます。二つの粒子を交換すると、ボソン系の波動関数は 変化しませんが、フェルミオン系の場合はマイナスの符号が付けられます。
$$\Psi_B(r_1, r_2)=\Psi_B(r_2, r_1),\ \ \ \Psi_F(r_1, r_2) = -\psi_F(r_2, r_1)$$
一方で、二次元空間における場合、波動関数が交換に使われる軌道に依存することがあり、空間の特徴によって、 波動関数に一般的な位相が付きます。
$$\Psi_A(r_1, r_2)=e^{i\theta}\Psi_A(r_2, r_1)$$
このような粒子はエニオンといい、分数統計に従います。数学的に、エニオンのような粒子の交換を扱う際に群を定義します。 波動関数に付く位相因子はその群の表現であり、この場合には絶対値1の複素数となっています。 しかし、3つ以上の粒子があり、かつ縮退もあれば、この群の表現は数ではなく、 縮退している状態を入れ換えたり混ぜたりする行列になります。 このような群で表される粒子は、非可換エニオンと呼ばれ、 非可換統計に従うことが知られています。また、このような議論はほとんどの場合、低次元で行われていますが、 三次元では点粒子ではなくテクスチャーをもったものにすると類似な議論ができます。マヨラナフェルミオン
マヨラナフェルミオンとは、1937年にE. Majoranaによって理論的に提案された、 粒子と反粒子が等しいフェルミオンです。ディラック方程式の実数解として存在し、 この解で表される粒子と反粒子は電荷をもたなくなります。 数学的に実数であるので複素数で表現される通常のフェルミオンの半分としてみなすことができます。 マヨラナ氏は、このような実数解の存在を理論的に示したが、 このような性質をもつ粒子は未だ発見されていません。 現在のところニュートリノやダークマターがこのようなフェルミオンの候補物質としてあがっていますが、 実験では確認されていません。 しかし、最近になって、我々の扱う凝縮系物理の分野でマヨラナフェルミオンが存在している可能性が指摘され、 大きな注目を集めています。
超伝導体では、電子とホールは重ね合わせ状態で存在し、準粒子の数が一定ではなくなります。 そのため、電荷はもはや良い量子数ではなく、あらゆる電荷をもつ準粒子が存在し得ます。 特に、電子とホールが完全に重なり合えばゼロ電荷の準粒子も実現可能です。 有効的なマヨラナ粒子を得るにはこの条件が必要となります。 しかしながら、通常の超伝導ギャップは、このような完全な重ね合わせを実現することはできず、 マヨラナフェルミオンの実現は期待できません。だが、トポロジカル超伝導の場合には違ってきます。 トポロジカル超伝導は、非自明なギャップをもち、超伝導体の端でギャップが閉じる、 つまり、端ではゼロエネルギー状態ができます。この状態は無電荷の電子とホールの重ね合わせ状態であり、 マヨラナフェルミオンに相当します。トポロジカル超伝導が自然に存在するか否かは、 単純な問題ではありませんが、最近の実験でそのような状態を人工的に創造し、 マヨラナ準粒子だと思われるものがコンダクタンスのピークとして観測されています。 まだ絶対的な証拠ではありませんが、凝縮系でマヨラナフェルミオンが存在することを大きく支える結果といえます。
凝縮系で実現するマヨラナ粒子に対する期待は特に大きいです。 その理由は、非自明な実現のため低次元では非可換統計に従う準粒子であるからです。 非可換エニオンなので、環境のノイズに対して強く、従来のディコヒーレンスがなく、 量子情報を非常に安定した形で保つことが可能と考えられています。 そのため、トポロジカル量子ビットとして将来の量子コンピュータに応用できる可能性が指摘されています。
-
単原子層物質 ▼
単原子層物質とは原子が1層からなる物質系のことで、「グラフェン」が実現してからグラフェンを超えるような物質を実現するため、 理論・実験の両面で爆発的に研究が進められています。代表する物質としてはグラフェン、MoS2、BN(boron nitride)などが挙げられます。 初の単原子層物質である「グラフェン」は2004年に合成され、2010年にノーベル物理学賞の対象となりました。 炭素がハニカム格子を組んだ極めて純度の高い2次元物質で、ゼロギャップ半導体となる特異な電子構造を持ち、 ディラクフェルミオンの存在が確認されており、高い移動度持つことから機能デバイスとして期待されています。
グラフェンはトポロジカル絶縁体の候補としてもあげられていますが、スピン軌道相互作用が小さいためにギャップをあけられず、 実験的に可能な温度で量子スピンホール効果を測定することができないという欠点があります。 そこで、注目を浴びているのが、グラフェンのシリコン・ゲルマニウム・スズの類似物質となる「シリセン」、「ゲルマネン」、「スタネン」です。 これらの物質は完全に2次元的なsp2混成軌道ではなくsp3に近い低バックル構造を持つためグラフェンにはない新しい物性を示し、 比較的大きなスピン軌道相互作用を持つことから電場や磁場でエネルギーギャップを自在に制御できるとして2次元トポロジカル絶縁体の候補として挙げられています。
-
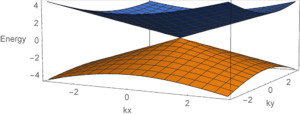
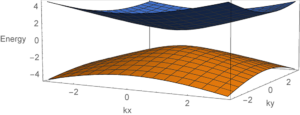
ワイル半金属 ▼
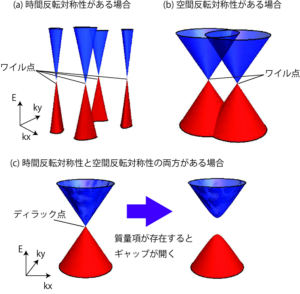
ワイル半金属中の電子は、低温で相対論におけるギャップレスのワイルフェルミオンのように振る舞うという特徴があります。 このとき縮退していない価電バンドと伝導バンドが一点において接触しており、その点のことをワイル点と呼びます。 このワイル点を得るためには少なくとも時間反転対称性か空間反転対称性を破っていなくてはなりません。 なぜならば、時間反転対称性と空間反転対称性が同時に存在するとき、ブリルアンゾーン内の任意のk点において2重縮退(クラマース縮退)が生じ、 接触点近傍の振る舞いはワイルフェルミオンではなくディラックフェルミオンとなるからです。 次節で説明するようにディラック点の場合、考えているk点が特殊な対称点に居ない限り、ギャップを開けるような質量項が存在し、 バンド反発によりギャップが開いた状態が安定となります。
この議論は以下のようにトポロジカル数を用いても説明することができます。ワイル点近傍の振る舞いは有効的に、$$H(k)=v(k_x\sigma_x+k_y\sigma_y+k_z\sigma_z)$$と書くことができます。 ここでv>0はフェルミ速度、σはスピン空間のパウリ行列です。 ハミルトニアンからすぐわかるように波数とスピンの方向は固定されています。 従って、スピンの期待値をベクトルとして記述するとk=0を中心にスピンのベクトルが湧き出しているように見えるのです。 他方、H(−k)の場合はベクトルの向きが反転し、逆にスピンのベクトルがk=0に吸い込まれているように見えます。 この湧き出しと吸い込みはワイル点が持つトポロジカル数(チャーン数)が非自明でることを意味しており、それぞれC=+1とC=−1を持ちます。 また、電磁気学とのアナロジーよりC=+1とC=−1を持つワイル点は、波数空間におけるモノポールと反モノポールとも呼ばれます。 ブリルアンゾーンの周期境界性より、チャーン数の総和はゼロでなくてはなりません(ニールセン・二宮の定理)。 よって、ブリルアンゾーン内ではモノポールと反モノポールが常にペアで存在します。 ここに先ほどの時間反転対称性と空間反転対称性の議論を加えてワイル点の安定性を考えてみましょう。 まず、時間反転対称性のみの場合、時間反転操作はk→−kかつσi→−σiという変換を許容すると k点と−k点にはC=+1を持つワイル点が存在します。また、反モノポールも同時に存在しなくてはならないためあるk′点と−k′点にC=−1を持つワイル点も存在します。 従って、この場合少なくとも4つのワイル点が存在することになります。次に空間反転対称性のみがある場合を考えましょう。 空間反転操作の下で波数はk→−kと変換するがスピンは不変です。 従って、k点にC=+1のワイル点が、−k点にC=−1のワイル点がそれぞれ存在します。 よって、この場合は少なくとも2つのワイル点が存在することになります。 最後に時間反転対称性と空間反転対称性が両方とも存在する場合を考えます。 このとき上の2つの場合を組み合わせた操作が可能となり、スピンのみをσi→−σiと変換させることができます。 従って、k点にC=+1とC=−1を持つワイル点が同時に存在し、互いにキャンセルします。 これはトポロジカルに自明になることを意味し、ギャップを開けることが可能となります。
ワイル点が非自明なトポロジカル数を持つことに起因して、表面にフェルミアークが現れます。 フェルミアークとは表面に現れるフェルミ面の”弧”であり、表面に射影したワイル点を結ぶように存在します。 フェルミアークはワイル半金属固有の性質であり、ワイル半金属である強い証拠を与えます。 近年発見された時間反転対称性を持つワイル半金属TaAs、NbAsにおいてもARPESによりフェルミアークが観測されています。 また、パイロクロア型イリジウム酸化物やHgCr22Se44などもワイル半金属の候補物質として注目を浴びています。 ワイル半金属では異常ホール効果やカイラルアノマリー、 電気磁気効果など様々な興味深い現象が理論的に予測されており、 次世代のトポロジカル物質として近年研究が盛んに行われています。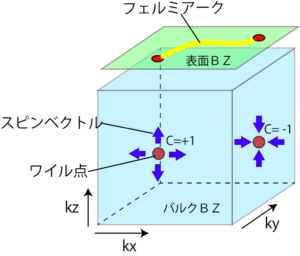 ワイル半金属を実現する系で最もシンプルなのが、トポロジカル絶縁体薄膜と磁性不純物をドープした通常の絶縁体薄膜の超格子構造です。 このとき磁性不純物によって時間反転対称性を破っており、磁化の方向は積層方向を向いています。 従って、この系は空間反転対称性を持つワイル半金属であり、ワイル点は少なくとも2つ存在することになります。 それぞれの絶縁体を薄膜にして積層しているため、トポロジカル絶縁体表面に現れるディラックコーンは上面と下面で混成を起こします。 このディラックコーン同士の混成の度合いを表すパラメータをΔT、ΔNと書き、 それぞれトポロジカル絶縁体薄膜と通常の絶縁体薄膜の膜厚に対応します。 ワイル半金属になるためには、磁性不純物の磁化の大きさが|ΔT−ΔN|より大きい必要があります。 従って、|ΔT−ΔN|が小さいとき、ワイル半金属になる可能性があります。 実際、|ΔT−ΔN|が0に近い物質としてiPCM (超格子型相変化メモリ)があります。 この物質はトポロジカル絶縁体と通常の絶縁体にそれぞれSb2Te3とGeTeを用いています。 特徴として温度を上げていくと結晶の構造転移が生じ、電気抵抗の高い相から低い相へ相転移することが知られています。 この2相の電気抵抗差を利用すればメモリとして活用できるため、近年次世代メモリとして産業的に注目を集めている。 第一原理計算の結果によると時間反転対称性と空間反転対称性を有する高抵抗の相において|ΔT−ΔN|の値がほぼ0になることが指摘されています。 従って、もし積層方向に磁化が向くように磁性不純物をドープできれば、ワイル半金属になる可能性があります。 しかし、今のところ実現されたという報告はされていません。
ワイル半金属を実現する系で最もシンプルなのが、トポロジカル絶縁体薄膜と磁性不純物をドープした通常の絶縁体薄膜の超格子構造です。 このとき磁性不純物によって時間反転対称性を破っており、磁化の方向は積層方向を向いています。 従って、この系は空間反転対称性を持つワイル半金属であり、ワイル点は少なくとも2つ存在することになります。 それぞれの絶縁体を薄膜にして積層しているため、トポロジカル絶縁体表面に現れるディラックコーンは上面と下面で混成を起こします。 このディラックコーン同士の混成の度合いを表すパラメータをΔT、ΔNと書き、 それぞれトポロジカル絶縁体薄膜と通常の絶縁体薄膜の膜厚に対応します。 ワイル半金属になるためには、磁性不純物の磁化の大きさが|ΔT−ΔN|より大きい必要があります。 従って、|ΔT−ΔN|が小さいとき、ワイル半金属になる可能性があります。 実際、|ΔT−ΔN|が0に近い物質としてiPCM (超格子型相変化メモリ)があります。 この物質はトポロジカル絶縁体と通常の絶縁体にそれぞれSb2Te3とGeTeを用いています。 特徴として温度を上げていくと結晶の構造転移が生じ、電気抵抗の高い相から低い相へ相転移することが知られています。 この2相の電気抵抗差を利用すればメモリとして活用できるため、近年次世代メモリとして産業的に注目を集めている。 第一原理計算の結果によると時間反転対称性と空間反転対称性を有する高抵抗の相において|ΔT−ΔN|の値がほぼ0になることが指摘されています。 従って、もし積層方向に磁化が向くように磁性不純物をドープできれば、ワイル半金属になる可能性があります。 しかし、今のところ実現されたという報告はされていません。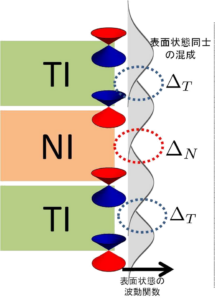 一方、トポロジカル絶縁体薄膜と絶縁体薄膜の超格子構造は絶縁体薄膜の上下に電位差をかけるだけでもワイル半金属相が現れることが知られています。 ここで、電位差は空間反転対称性を破る役割をします。 従って、ワイル点の数は積層方向に対する離散回転対称性に依存しますが、時間反転対称性持つワイル半金属であるから、少なくても4つ存在することになります。
一方、トポロジカル絶縁体薄膜と絶縁体薄膜の超格子構造は絶縁体薄膜の上下に電位差をかけるだけでもワイル半金属相が現れることが知られています。 ここで、電位差は空間反転対称性を破る役割をします。 従って、ワイル点の数は積層方向に対する離散回転対称性に依存しますが、時間反転対称性持つワイル半金属であるから、少なくても4つ存在することになります。 -
ディラック半金属 ▼
ディラック半金属は時間反転対称性と空間反転対称性が保存されているときに現れます。 このとき任意の波数kにおいて2重縮退(クラマース縮退)が生じ、伝導バンドと価電バンドの接触点(ディラック点)で4重縮退が実現されます。 接触点近傍では、低温においてギャップレスのディラックフェルミオンのように振る舞うことが知られています。 ワイル半金属のページで解説したように、ディラック点はトポロジカルに保護されておらず、容易にギャップを開けることができます。 しかし近年、空間反転対称性と時間反転対称性に加えて結晶対称性が存在すると安定なディラック点が存在することが示されました。 ここでは最近発見されたディラック半金属を念頭に置き、離散回転対称性: Cn(n=2,3,4,6)によってディラック点が安定化される場合を考えます。 離散回転対称性により保護されるディラック点には大きく分けて2通りあります。1つはブリルアンゾーン境界の時間反転対称点(TRIM)にディラック点が1つ存在する場合です。 このとき結晶は非共型対称性を持つ必要があります。このタイプの候補物質はβ-cristobalite BiO2(C4対称性)や歪んだスピネル構造(C2対称性)です。 他方、もう1つは対称軸上に2つのディラック点が現れる場合です。 このときディラック点はTRIMから離れたところにできます。 このタイプはBi3Na(C3対称性)[6-8]やCd3As2(C4対称性)の物質においてARPESやSTMによりディラック点が実験的に観測されています。 他にもA3Bi(A=Na, K, and Rb)やBaYBi(Y=Cu, Ag, and Au)でディラック点が存在することが第一原理計算により示されています。 また、後者のタイプには回転軸に対して平行に表面を作るとワイル半金属と同様に2つのディラック点の間に表面状態が現れます。 Bi3NaのようにC3により保護されている場合は回転軸に対して垂直な平面にZ2トポロジカル数が存在し、フェルミアークのペアが現れます。 他方Cd3As2のようにC4で保護されている場合は回転軸に対して垂直な鏡映面に非自明なミラーチャーン数が存在し、フェルミループが現れます。 ここでフェルミループはフェルミアークと異なり、表面に射影したディラック点に繋がっていない。 後者のディラック半金属は非自明な表面状態を持つことからしばしば「トポロジカルディラック半金属」と呼ばれています。
ディラック半金属はトポロジカル絶縁体や、トポロジカル超伝導体、ワイル半金属、アクシオン絶縁体など様々トポロジカル相へのトポロジカル相転移が可能な物質として期待されています。 またグラフェンの3次元版としても注目を集めており、高い移動度や巨大な磁気抵抗が観測されていいます。
- アクシオン絶縁体
Cold atoms
 電気的に中性な原子を光や磁場により真空中に捕獲し希薄な気体状態に保って冷却すると、固化・液化することなく気体のまま超低温に至ります。近年、レーザー冷却・蒸発冷却の技術によりこのような超低温気体が実現し、人工的に自在に制御できる量子多体系として基礎研究・応用の両側面から注目を集めています。
電気的に中性な原子を光や磁場により真空中に捕獲し希薄な気体状態に保って冷却すると、固化・液化することなく気体のまま超低温に至ります。近年、レーザー冷却・蒸発冷却の技術によりこのような超低温気体が実現し、人工的に自在に制御できる量子多体系として基礎研究・応用の両側面から注目を集めています。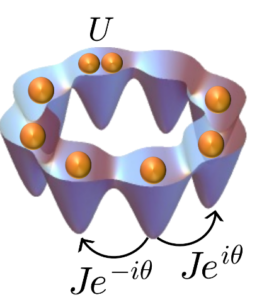 また、磁場や周波数の測定においては巨視的な数の原子が応答することにより感度が格段に高くなるため、高感度磁力計や原子時計を超える超高精度時計の開発といった応用も期待されます。このように、操作性の高い多体量子系である冷却原子気体は、『人工量子気体』とも呼ばれ、状況設定次第で実に様々な物理現象を研究できる舞台となっています。本研究室では、このような系を対象に、数値シミュレーションによる定量的な計算から、トポロジー・ホモトピー・群論といった数理物理よりの研究まで、幅広く取り組んでいます。以下では当研究室で扱っている研究テーマをキーワード解説としてご説明します。クリックで詳細が表示されます。
また、磁場や周波数の測定においては巨視的な数の原子が応答することにより感度が格段に高くなるため、高感度磁力計や原子時計を超える超高精度時計の開発といった応用も期待されます。このように、操作性の高い多体量子系である冷却原子気体は、『人工量子気体』とも呼ばれ、状況設定次第で実に様々な物理現象を研究できる舞台となっています。本研究室では、このような系を対象に、数値シミュレーションによる定量的な計算から、トポロジー・ホモトピー・群論といった数理物理よりの研究まで、幅広く取り組んでいます。以下では当研究室で扱っている研究テーマをキーワード解説としてご説明します。クリックで詳細が表示されます。-
ボース・アインシュタイン凝縮体(BEC) ▼
ボース粒子の集団を冷却すると、巨視的な数の粒子が単一の量子状態に凝縮するというボース・アインシュタイン凝縮が起こります。ボース凝縮を起こした物質をボース・アインシュタイン凝縮体(BEC)と呼びます。ひとたびボース凝縮が起こると、一つの一粒子状態に巨視的な数の粒子が凝縮するため、粒子集団が全体として一つの波のように振る舞い、量子性が顕著に現れます。古くからBECとして知られた超流動ヘリウムでは粘性ゼロで流体が流れるという超流動現象が起こりますが、これも巨視的波動関数の帰結の一つです。原子気体のBECでは、波動関数がレーザー等を用いて直接観測でき、2つのBECの干渉や渦の量子化といった物質波としての性質が実験で観測されています。
-
スピノールBEC ▼
原子気体では、異なる二種類のボース原子からなる混合気体や、単一の原子でもスピン状態の異なるものが混ざった状態でBECを作ることができます。このような内部自由度を持ったBECは、秩序変数(粒子の凝縮する波動関数)として複数の成分が必要で、スピノールBECと呼ばれます。特に、内部自由度が本物のスピンである場合には、スピン超流動という面白い状況が実現し、粒子と同様にスピンが散逸なく輸送されたり、スピンの空間変化により粒子の流れが生じたりします。最近では、スピン軌道相互作用やスピンに依存した複雑なゲージ場を人工的に作り出すことで、磁気スキルミオンのようなスピンの空間構造やトポロジカル絶縁体と同様の非自明なバンド構造が現れることが議論されています。
関連論文
-
ダイポールBEC ▼
電気的に中性な原子ではクーロン相互作用が働かないため、一般に2原子が原子サイズ程度の近距離に来たときのみ相互作用が働きます。しかし、原子が大きな磁気モーメントを持つ場合には、遠方まで働く磁気的双極子‐双極子相互作用が支配的となり、従来の原子気体とは全く異なる振る舞いが期待されます。近年、Cr, Er, Dy, Euといった磁気モーメントの大きな原子のBECが次々と実現し、新しい物性を示す凝縮体として注目されています。特に、スピン自由度を持ったBECではスピンの方位が空間変化することにより超流動カレントが生じ、スピン、軌道、ゲージの自由度の複雑に絡み合った現象が起こります。例えば、磁場中でスピン偏極した原子気体を用意した後、磁場を切ると、スピン角運動量が軌道角運動量へと転化し、凝縮体は回転を始めるというアインシュタイン-ド・ハース効果が起こります。この現象は、磁気モーメントが回転運動と同じ角運動量という物理量であることの証拠にもなっています。
関連論文
-
非エルミート・動的不安定性 ▼
通常、量子力学におけるハミルトニアンはエルミートであり、エネルギー固有値は実数となります。しかし、BECの励起スペクトルにはたびたび複素数のエネルギーが生じます。これは、ボース粒子の生成・消滅演算子の交換関係に由来して、準粒子のエネルギースペクトルが非エルミート行列で記述されるためです。エネルギーが複素数になると、時間とともに特定の励起が指数増大し、系が不安定となります。このような不安定性は動的不安定性と呼ばれ、実験でも様々な状況下で観測されています。最近の物性物理の研究では、外界との相互作用を現象論的に非エルミート性として記述して、新奇な量子状態を探索するという研究が多くなされていますが、ボース粒子系は微視的に非エルミート性を導出できる稀有な系であり、非エルミート系の物性解明に重要な系として位置づけられています。
関連論文
-
フロケ系・駆動系 ▼
電磁波や振動磁場といった時間周期的に振動する外場を系に作用させることで、量子状態やそのダイナミクスを制御することができます。空間周期的な系については、ブロッホの定理により運動量空間にも周期性が現れることがよく知られていますが、その時間版であるフロケの定理によると、時間周期的な系においては、エネルギー空間に周期性が現れます。これは、振動外場下では、その周波数に相当するエネルギーΔEを系が吸収・(誘導)放出することでエネルギーにΔEの整数倍の不定性が生じるためです。つまり、振動外場を印加するとスペクトルが折りたたまれ、新たなバンド交差が生じます。これを利用してバンドトポロジーの制御や、共鳴現象、動的不安定性のON/OFFなどが可能となります。
関連論文
-
トポロジカル相 ▼
バルクでエネルギーギャップを持つ絶縁体は、バルクでのギャップを閉じない連続変形によって移り合う系を同一視すると、自明な絶縁体(真空)に連続変形できてしまうトポロジカルに自明な相と、それには連続変形できないトポロジカルに非自明な相に分かれます。このトポロジーによる相の分類において本質的なのは、何らかの行列の固有値分布に「ギャップ」が存在することであり、系の詳細は重要ではありません。つまり、トポロジカル相は絶縁体に限らず、超伝導体や冷却原子系など、あらゆる系において実現します。近年、上で述べた平衡状態のトポロジカル相にとどまらず、フロケ系や非エルミート系などの非平衡系においても、トポロジカル相の物理が盛んに研究されています。中でも、系のパラメーターや粒子の散逸を高精度で制御できる冷却原子系は、新奇なトポロジカル相を実現し得る理想的なプラットフォームとして注目を集めています。
関連論文
-
開放量子系 ▼
学部生の授業で習った、シュレディンガー方程式によって記述される通常の量子力学は、システムが他の物理系である環境とは断絶された、極めて理想化された状況である孤立量子系を取り扱います。それに対して現実の量子系では、システムは環境と常に相互作用をしています。そのような系が開放量子系です。例えば、励起状態にある原子(システム)が、真空(環境)と相互作用をすることで、光を放出しながら自発的に低エネルギー準位に落ち込む自然放出は、シュレディンガー方程式の枠組みを超えて、開放量子系として取り扱う必要があることが知られています。
-
光格子系・動的ゲージ場 ▼
冷却原子気体では、光の波としての性質を用いた理想的な格子系を作ることができます。この系では、光子振動(フォノン)が無く、格子間距離も自在に変更できるため、新たな実験系におけるプラットフォームを提供しています。冷却原子系での実験においては電気的に中性な原子を扱っているため、電場(ゲージ場)などの相互作用を直接的に取り入れることができません。そこで、隣接する格子サイトへ飛び移る際に位相差をつけることで、アハロノフ・ボーム効果のように仮想的なゲージ場を導入することが提案されました。近年では電磁場のU(1)ゲージ場が実験において再現されており、またSU(N)やZ₂などの対称性を持つゲージ場の導入も、理論的に提唱されてきています。
Magnetic skyrmions
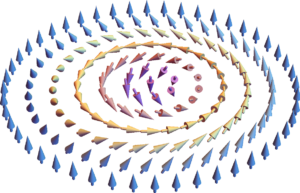 磁気スキルミオンとは、磁化ベクトルが2次元実空間において右図に示すような空間構造をとったもので、多数のスピンが全体で一つの粒子のように振る舞うという特異な性質を示します。この性質は、スキルミオン構造がトポロジカルに安定な構造であることに由来し、空間各点の磁化の振幅を有限に保ち、かつ境界条件(右図の場合、外周で磁化が上を向く)を満たすような連続変形ではスキルミオンをほどくことができません。つまり、ひとたびスキルミオンができれば勝手に消えることはできずに安定に存在し続けます。
磁気スキルミオンとは、磁化ベクトルが2次元実空間において右図に示すような空間構造をとったもので、多数のスピンが全体で一つの粒子のように振る舞うという特異な性質を示します。この性質は、スキルミオン構造がトポロジカルに安定な構造であることに由来し、空間各点の磁化の振幅を有限に保ち、かつ境界条件(右図の場合、外周で磁化が上を向く)を満たすような連続変形ではスキルミオンをほどくことができません。つまり、ひとたびスキルミオンができれば勝手に消えることはできずに安定に存在し続けます。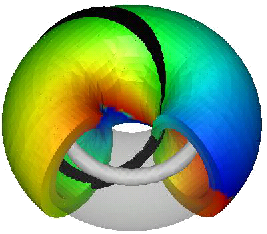 本研究室では、これまでに、カイラル磁性体/強磁性体接合系における磁化構造や、スキルミオン間相互作用の制御、結晶磁気異方性により歪んだスキルミオンのダイナミクスなどについて研究してきました。また最近、Hopfionと呼ばれる3次元空間におけるS²場のトポロジカル構造が観測され、新たなトポロジカル構造として注目しています。Hopfionは結び目の絡み数で分類される励起で、スキルミオンとは異なるトポロジーを持っており、今後の展開が期待される系の一つです。また、磁性体でのHopfionが議論される以前に、川口が提案した方法により冷却原子気体でHopfionが観測されており、分野横断的な研究でもあります。
本研究室では、これまでに、カイラル磁性体/強磁性体接合系における磁化構造や、スキルミオン間相互作用の制御、結晶磁気異方性により歪んだスキルミオンのダイナミクスなどについて研究してきました。また最近、Hopfionと呼ばれる3次元空間におけるS²場のトポロジカル構造が観測され、新たなトポロジカル構造として注目しています。Hopfionは結び目の絡み数で分類される励起で、スキルミオンとは異なるトポロジーを持っており、今後の展開が期待される系の一つです。また、磁性体でのHopfionが議論される以前に、川口が提案した方法により冷却原子気体でHopfionが観測されており、分野横断的な研究でもあります。関連論文
